A simple model for plug flow processes with heat transfer and phase change

Computational Fluid Dynamics is becoming a powerful and well accepted tool for optimizing the flow patterns in industrial equipment. This article develops a simple mathematical model for plug flow, which is applicable to the development of the flow in furnace tubes, packed vessels and other geometries.

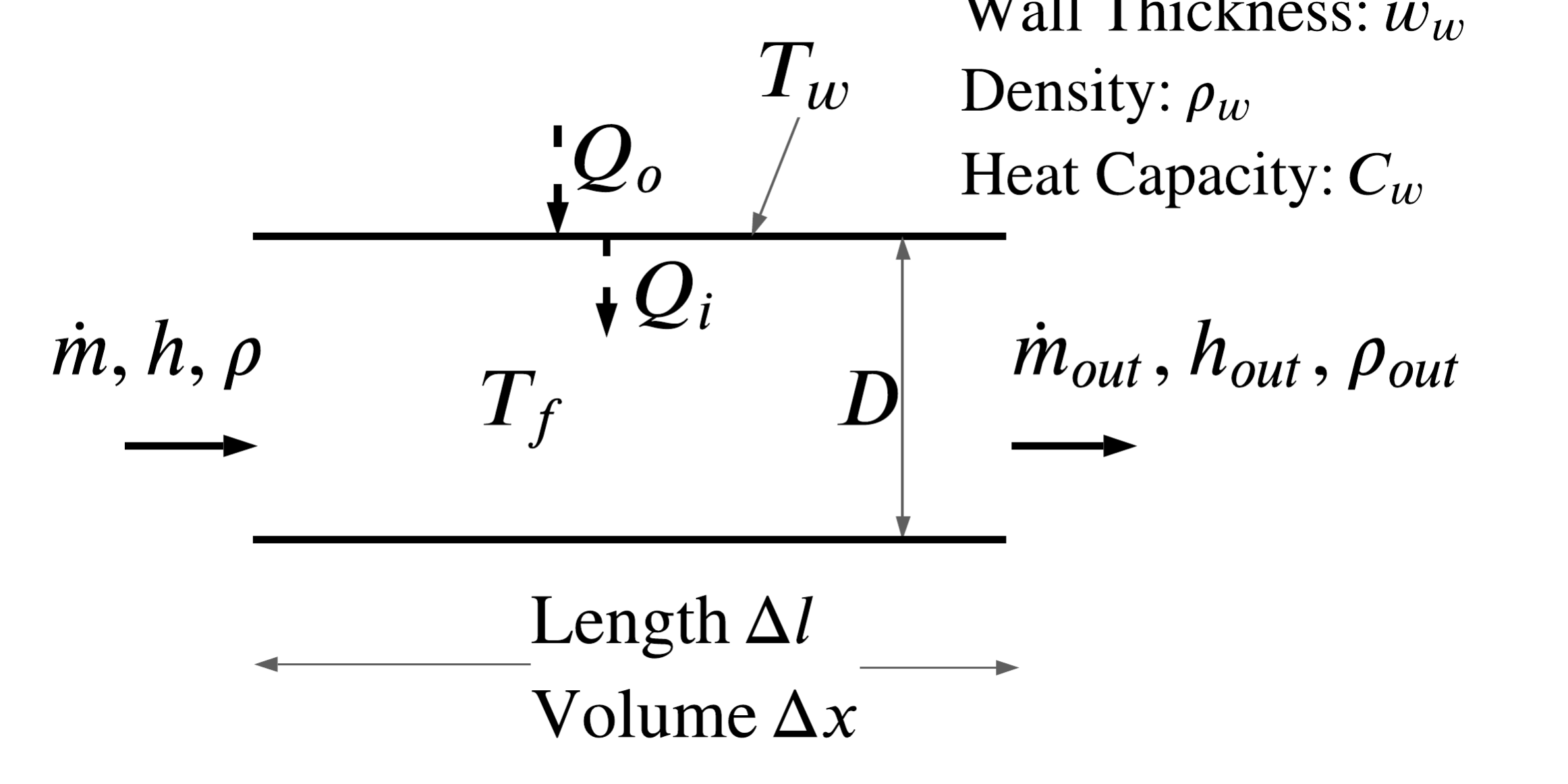
Our geometry considered is:

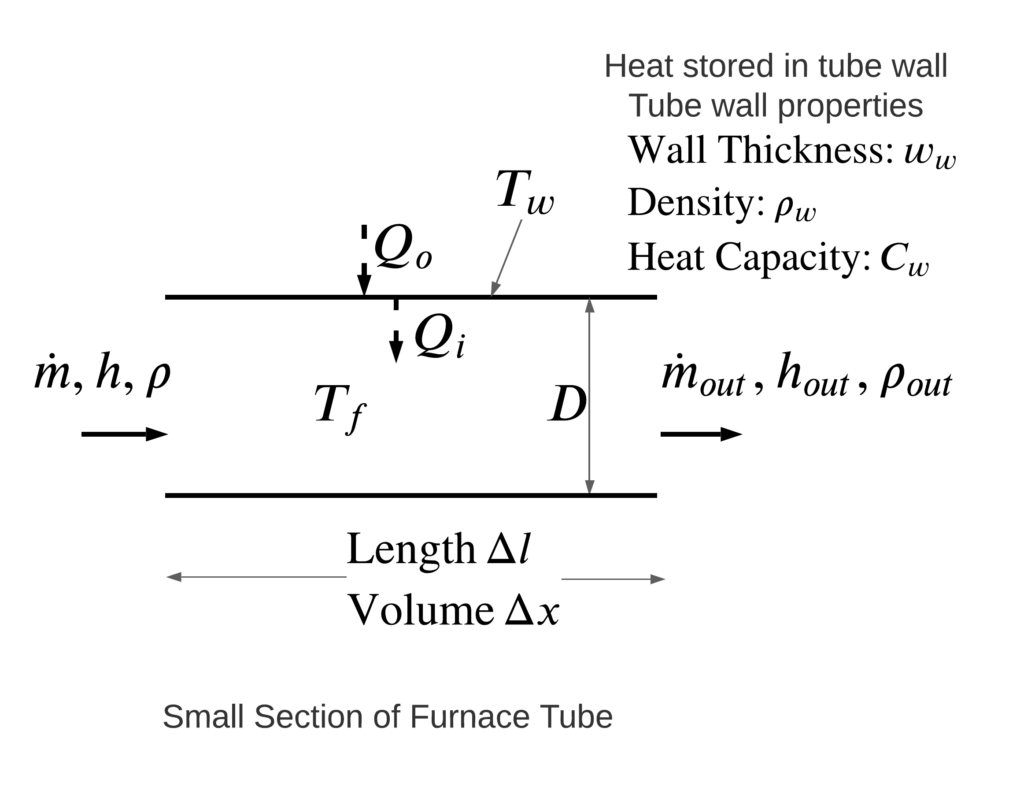
The flow process is dictated by conservation of mass, conservation of energy, and an equation of state. We will consider the process operates at constant pressure as a convenient simplification.

Equation of State

The equation of state relates the specific volume to the enthalpy of the fluid. We will assume a linear relationship in the sub cooled, two-phase and superheated regions.

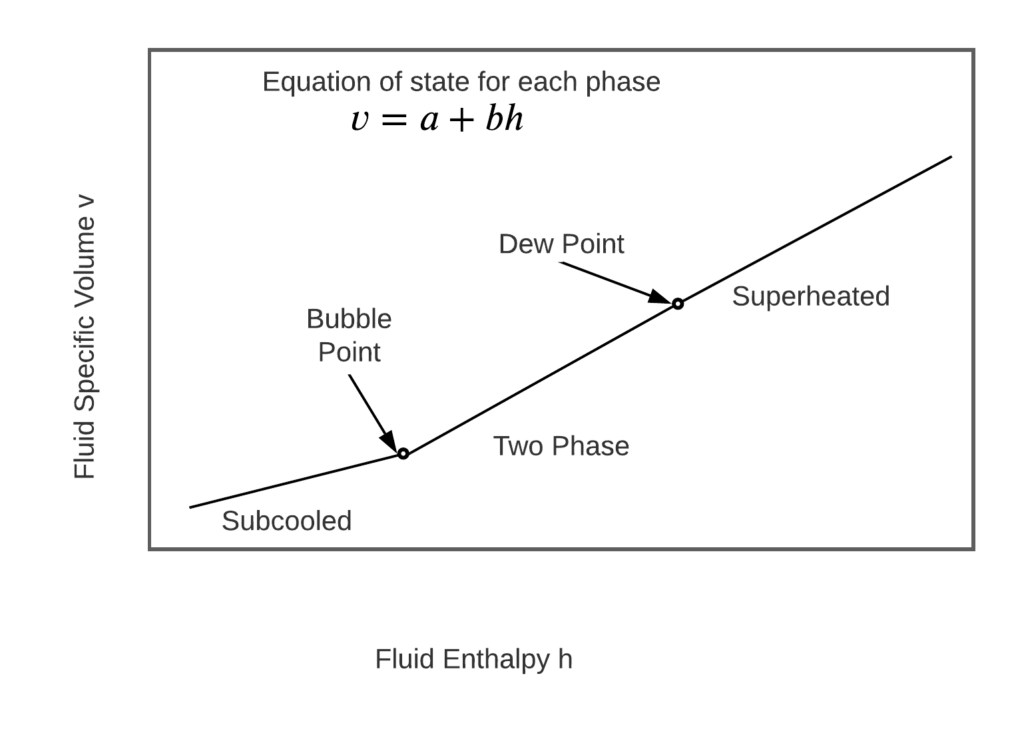
The linear relation is perfect for the two phase region, and fairly accurate for the sub cooled and superheated regions if we are willing to accept small deviations from the actual specific volume or density. Since the important phenomena occurs in the two phase region, this assumption is acceptable.

Governing equations

The differential equations for the conservation of mass and energy are:

∂ρ/∂t + ∂uρ/∂x = 0

∂ρh/∂t + ∂uρh/∂x = Q”

Most finite volume schemes will solve these two conservation laws simultaneously with the equation of state. Instead, we will use the conservation of mass only in the finite volume scheme. A bit of calculus is needed to convert the conservation of energy into a useful equation for the volumetric flow.

We need to simplify the energy balance, so break it up with chain rule

ρ ∂h/∂t + h ∂ρ/∂t + h ∂ρu/∂x + ρu ∂h/∂x = Q”

Cancel out the terms that are common with the conservation of mass:

Most finite volume schemes will solve these two conservation laws simultaneously with the equation of state. Instead, we will use the conservation of mass only in the finite volume scheme. A bit of calculus is needed to convert the conservation of energy into a useful equation for the volumetric flow.

We need to simplify the energy balance, so break it up with chain rule

ρ ∂h/∂t + h ∂ρ/∂t+ h ∂ρu/∂x + ρu ∂h/∂x = Q”

Cancel out the terms that are common with the conservation of mass:

Most finite volume schemes will solve these two conservation laws simultaneously with the equation of state. Instead, we will use the conservation of mass only in the finite volume scheme. A bit of calculus is needed to convert the conservation of energy into a useful equation for the volumetric flow.

We need to simplify the energy balance, so break it up with chain rule

ρ ∂h/∂t + h ∂ρ/∂t+ h ∂ρu/∂x + ρu ∂h/∂x = Q”

Cancel out the terms that are common with the conservation of mass:

∂h/∂t + u ∂h/∂x = (1/ρ) Q”

Note that density is related to volume, and write this in substantial form.

Dh/Dt = v Q”

Now write the material balance equation using the substantial derivative.

∂ρ/∂t + u ∂ρ/∂x + ρ ∂u/∂x=0

Dρ/Dt = -ρ ∂u/∂x

Use the relationship between density and specific volume (ρ = 1/v, ∂ρ = -(1/v) ∂v).

Dv/Dt = v ∂u/∂x

Now recognize that we can use the EOS to relate a small change in enthalpy to a small change in specific volume.  (Dh = (1/b) Dv). The substantial derivative for the conservation of energy becomes

Dv/Dt = v b Q”

Equate the two substantial derivatives for specific volume.

∂u/∂x = b Q”

We now have an ordinary differential equation for the volumetric flow across the domain. This depends on the boundary condition (inlet volumetric flow), the heat flux and the expansion coefficient.

Wall Temperature

We also need an equation for the evolution of the wall temperature.

First we need to relate the heat flux per unit area Q’ to heat flux per unit tube volume Q”

Q” L π /4 D² = Q’ L π D

Q” L D/4 = Q’

The balance equation for the wall temperature is:

ρ C_w π D w L ∂T_w/∂t = π D² L (Q_o”−Q”)

ρ_w C_w w ∂T_w/∂t = D (Q_o”−Q”)

The rate equation for the inside heat flux is

πD²/4 Q” = π D U (T_w − T)

D Q” = 4 U (T_w − T)

We have two equations that are used to evolve the tube wall temperature and inside heat flux over time.

Solution

Our transient thermo-hydraulics problem is described by a homogeneous conservation law with variable coefficients, literally a text book example in Randy LeVeque’s book.

This model is solved quickly using Python on an underpowered laptop or a Chromebook.

References

Randall J. LeVeque, Finite Volume Methods for Hyperbolic Problems, Cambridge University Press in 2002. https://depts.washington.edu/clawpack/book.html